Note technique
Cancer/Rodiother 1998 2 392-403 © Elsevier, ParisUtilisation d'un collimateur multilames
pour la production de faisceaux modulés en intensité
S Papatheodorou, JC Rosenwald*, ME Castellanos, S Zetkili, L Bonvalet, G
Gaboriaud
Service de physique médicale, institut Curie, 26, rue d'Ulm,
75248 Paris cedex 05, France
RÉSUMÉ
En radiothérapie externe la modulation d'intensité permet d'une
part de compenser les variations d'épaisseur et l'influence des hétérogénéités, et
d'autre part, lors de l'association de plusieurs faisceaux, d'obtenir une distribution de
dose précisément adaptée à la forme du volume cible. Les collimateurs multilames
offrent la possibilité de réaliser cette modulation d'intensité en jouant sur la
position des lames en fonction du temps. Cette méthode, rendue possible par les
développements de la technologie des accélérateurs et de l'informatique, présente
plusieurs avantages par rapport à d'autres, tels que les filtres compensateurs. Nous
avons mis au point un logiciel permettant le calcul de la relation entre position de lames
et nombre d'unités moniteur pour obtenir une distribution d'intensité donnée, et
l'avons appliqué à un accélérateur Varian, équipé d'un collimateur comportant 40
paires de lames. L'analyse des résultats expérimentaux démontre la faisabilité et le
potentiel de la méthode. © 1998 Elsevier, Paris
radiothérapie conformationelle I collimation dynamique I modulation d'intensité
SUMMARY
The use of a multileaf collimator for the
generation of intensity-modulated beams.
In external radiotherapy, the use of intensity modulated fields bas been proposed for
tissue and non-homogeneity compensation or for the generation of conformal dose
distributions. Multileaf collimators can be employed dynamically for the modulation of the
X-ray field in two dimensions. Efficient dynamic collimation became possible due to
advances in computer and linear accelerator technology. It presents a number of advantages
over conventional methods such as the use of compensators. We have developed a program
which calculates, from a given intensity distribution, the motion of the MLC leaves as a
function of monitor units, and we have applied it on a Varian linear accelerator with a 40
pair multileaf collimator. The analysis of the experimental results demonstrates the
feasibility and the potential of the method. © 1998 Elsevier, Paris
conformal radiotherapy / dynamic collimation intensity modulation
La radiothérapie de conformation représente une avancée importante de l'oncologie moderne. Elle consiste à délivrer précisément dans le volume-cible une dose très élevée, en irradiant très peu les structures saines avoisinantes [36]. Bien que l'ambition de la mettre en œuvre remonte aux débuts de la radiothérapie, elle est devenue réalisable grâce à la convergence des progrès dans les domaines de la technologie des accélérateurs, des systèmes de calcul de dose, de l'imagerie médicale et de l'assurance de qualité [2, 4, 7, 15, 24, 28, 34, 36]. Les moyens techniques et théoriques mis en œuvre incluent la définition précise du volume cible par imagerie numérique (essentiellement tomodensitométrie), une collimation spécifique du faisceau, des calculs de dose dans les trois dimensions de l'espace, des procédés d'optimisation, et une contention rigide du patient avec vérification de sa position.
Il est actuellement évident que les distributions de dose produites par un ensemble de faisceaux de photons Modulation d'intensité par collimateur rnultilames peuvent être nettement améliorées par l'application d'une modulation d'intensité à chaque faisceau [3, 5, 7, 18, 34, 35, 38]. L'utilisation de faisceaux modulés en intensité a été initialement proposée par Brahme et al [8] et davantage développée par Cormack [12,13] et Barth [1]. Ils ont utilisé des méthodes analytiques afin de calculer la distribution de la fluence incidente nécessaire pour délivrer la distribution de dose prescrite (ce problème est connu sous le nom de " problème inverse"). De nombreux auteurs se sont également consacrés à des techniques de résolution numérique [2, 5, 7, 34, 35], abordant pour la plupart le problème de l'optimisation des paramètres d'irradiation par l'utilisation de critères physiques et biologiques. Pour réaliser en pratique la distribution de fluence désirée, la modulation d'intensité se révèle alors être un élément indispensable [2, 5, 18, 34-36]. Mais, même dans le cas de la radiothérapie externe classique, on est amené à modifier la répartition de la dose dans un plan perpendiculaire à l'axe du faisceau, pour compenser à la fois la forme de la surface d'entrée et les hétérogénéités de l'organisme. On obtient ainsi une dose homogène à une profondeur donnée.
Il existe plusieurs moyens pour obtenir des faisceaux modulés en intensité [38]. La méthode la plus simple, est l'utilisation de filtres compensateurs placés au niveau du porte-caches. Depuis les années 60, le principe de l'utilisation du compensateur est resté le même, mais des améliorations ont été apportées à l'acquisition des données du patient, au calcul précis du compensateur et de la dose en présence de cet accessoire [26, 311. Néanmoins, l'utilisation des compensateurs n'est pas dépourvue d'inconvénients. Des compensateurs individuels doivent être fabriqués pour chaque faisceau, ce qui est coûteux et parfois difficile à réaliser. De plus, le temps total du traitement est augmenté, car il est nécessaire d'entrer dans la salle du traitement pour changer les compensateurs entre les irradiations. En dernier lieu, l'utilisation de compensateurs rend difficile le calcul précis de la dose, car il faut prendre en compte la production de photons diffusés et le durcissement du faisceau [9].
Plus récemment, l'utilisation du balayage du champ par un faisceau élémentaire a été proposée, pour la production de faisceaux modulés en intensité [6, 17, 21, 22, 27]. Cette technique est réalisable seulement avec certains appareils de traitement, comme le Scanditronix MM50TM Racetrack Microtron. La tête de l'appareil contient un système contrôlé par ordinateur qui effectue le balayage d'un faisceau élémentaire et construit le champ d'irradiation par constitution d'une matrice de faisceaux élémentaires d'intensité variable. Un ensemble d'aimants de balayage produit des faisceaux d'électrons ou de photons de haute qualité sans avoir recours à des diffuseurs ou des égalisateurs. Néanmoins en pratique, la précision du profil d'intensité obtenu est limitée par la largeur de la Gaussienne de chaque faisceau élémentaire.
Cette restriction peut être surmontée par l'utilisation combinée de faisceaux élémentaires par balayage et d'une collimation dynamique par collimateur multilames [17, 27].
Une autre technique basée sur le principe d'un balayage mécanique du champ pour la production des faisceaux modulés en intensité, est celle appelée "tomothérapie". Cette technique repose sur l'utilisation d'une " bande" étroite (fan beam) de photons de haute énergie, tournant autour d'un anneau dans lequel le patient est déplacé continuellement. Le principe de cette technique est analogue à celui de la scanographie hélicoïdale. L'intensité de la "bande" est modulée par un collimateur dynamique constitué de plusieurs paires de petites lames qu'on peut interposer ou pas dans le faisceau [23]. Bien que la technique de " tomothérapie " soit très élégante, elle nécessite l'utilisation de dispositifs spéciaux, tels que le système " Nomos Peacock ". Le temps total du traitement est très élevé pour des volumes cibles importants, et des problèmes de chevauchement de coupes peuvent apparaître dans le sens longitudinal.
La modulation d'intensité peut également être produite par l'utilisation dynamique d'un collimateur multilames (MLC). Les premiers efforts dans le domaine de la collimation dynamique étaient considérablement limités par la technologie des ordinateurs et des accélérateurs disponibles. Toutefois, des modulations simples de la distribution de la fluence pouvaient être obtenues par le mouvement des mâchoires asymétriques pendant l'irradiation. La simulation d'un filtre en coin grâce au mouvement d'une mâchoire, appelé filtre en coin dynamique, a été présentée par Kijewski et al, en 1978 [19] et Leavitt et al, en 1990 [20]. Cette réalisation simple de la collimation dynamique est aujourd'hui proposée de manière standard par plusieurs constructeurs d'accélérateurs linéaires.
Bortfeld et al [3] et Galvin et al [14] ont proposé la production de faisceaux d'intensité modulée par superposition partielle d'un nombre fini de faisceaux statiques définis par collimateur multilames. Geis et al [16] ont présenté l'utilisation d'une séquence de sous-champs définis par collimateur multilames pour la production de faisceaux compensés, en imitant les caractéristiques d'atténuation d'un compensateur physique.
Toutefois, une véritable collimation dynamique efficace n'est devenue possible que grâce aux mouvements indépendants et à vitesse variable des lames du collimateur multilames. Cette technique peut être appliquée aux accélérateurs dont le déplacement des lames est contrôlé par ordinateur et peut être effectué pendant l'irradiation. Les lames doivent avoir la capacité de dépasser l'axe du collimateur. Plusieurs techniques pour la mise en pratique de la collimation dynamique ont été proposées. Les plus importantes sont la technique de fermeture (close in) et la technique de la fenêtre glissante (sliding window) [10, 16, 33, 38]. La technique de fermeture consiste à positionner les lames de part et d'autre d'un maximum local de la distribution de la fluence souhaitée. Dès le lancement du faisceau, les lames se déplacent vers un point central. Au cours d'une seule irradiation, le mouvement d'une lame gauche vers la droite produit la partie croissante du profil (comme dans le cas des filtres en coin dynamiques). En même temps, le déplacement d'une lame droite vers la gauche, produit la partie descendante du profil. Leur combinaison crée un profil comportant un seul maximum. De telles contraintes limitent considérablement le type des champs d'intensité modulée qui pourraient être obtenus pendant une seule irradiation. En effet, un profil arbitraire avec plusieurs maxima et minima doit être divisé en plusieurs parties produites séparément par des irradiations différentes. Le faisceau doit être arrêté pendant le repositionnement des lames avant chaque partie. Cette procédure augmente donc le temps du traitement et elle rend le calcul des trajectoires des lames difficile. De plus, la précision du profil produit par la méthode close-in, dans les régions de fort gradient, est limitée par la vitesse mécanique des lames et par le débit de la dose. Certains profils ne restent ainsi qu'approximatifs. Ces inconvénients ont conduit les chercheurs à préférer la technique de la " fenêtre glissante" qui présente théoriquement comme seul inconvénient l'augmentation du temps d'irradiation. Dans la technique de la fenêtre glissante, les deux lames opposées de chaque paire démarrent du même côté du champ et se déplacent dans un seul sens vers l'autre côté, mais avec des vitesses différentes. Convery and Rosenbloom [11] ont présenté une version de la technique de la fenêtre glissante, dans laquelle la détermination des trajectoires des lames est traitée comme un problème de minimisation en programmation linéaire sous contraintes. La fonction objective à minimiser est le temps total d'irradiation et l'algorithme d'optimisation utilisé l'algorithme Simplex [25]. Le problème de cette approche est la durée importante du temps nécessaire au calcul des trajectoires des lames. Plus récemment, d'autres groupes de chercheurs [27, 29, 30], ont résolu ce même problème en utilisant des procédures itératives, qui permettent des temps de calcul de quelques millisecondes. La technique sliding window apparaît, ainsi, comme la plus efficace pour la collimation dynamique.
Cet article présente la mise en œuvre de la méthode de la fenêtre glissante pour la production de faisceaux modulés en intensité ainsi que sa validation expérimentale, avec simulation du déplacement continu par superposition de champs individuels délimités par un collimateur comportant 40 paires de lames1.
1 Accélérateur linéaire Clinac 2300CD et collimateur multilarnes Varian - Varian Médical France.
MÉTHODES ET MATÉRIEL
Logiciel
Le logiciel de base que nous avons développé permet le calcul de la relation entre position des lames et nombre d'unités moniteur (UM) pour obtenir un faisceau d'intensité modulée.La collimation dynamique repose sur le principe selon lequel on peut utiliser des lames qui se déplacent pendant l'irradiation pour déterminer le temps d'exposition en un point donné. Les principes de l'algorithme de la collimation dynamique sont analysés pour des profils monodimensionnels, représentés par N points discrets et équidistants. L'extension de l'algorithme aux modulations d'intensité bidimensionnelles, se fait facilement, en appliquant la méthode monodimensionelle indépendamment pour chaque paire de lames. On su pose que les profils de dose désirés correspondant à chaque paire de lames opposées ont été préalablement déterminés par une autre application. Il peut s'agir soit d'un système qui et calcule les épaisseurs d'un compensateur-photons à partir d données anatomiques, soit d'un programme de calcul " inverse" qui permet la détermination de la modulation optimaIe de chaque faisceau permettant d'obtenir globalement distribution des doses voulue. La modulation de la fluence souhaitée le long de chaque paire de lames est donc le point de départ des calculs.
Le problème à résoudre est de calculer les trajectoires des lames qui produisent le profil souhaité dans le temps le plusi court possible. Pour cette approche, nous avons fait les hypothèses suivantes:
- la source est ponctuelle, et la distribution de la fluence incidente (avant la collimation dynamique) est homogène;
- la source d'irradiation délivre un débit de fluence constant;
- l'accélération et la décélération des lames sont infinies;
- la transmission à travers les lames est négligeable;
- les fuites entre les lames sont négligeables;
- la contribution du rayonnement diffusé est négligeable;
- la modification de la fluence due à chaque lame est indépendante de la position des autres lames.
Pour une paire de lames donnée, qui se déplace le long l'axe x vers la droite, la lame droite (qui se déplace en premier est nommée " lame B " et la lame gauche (qui suit) est nommée " lame A ". F(x) est la distribution de la fluence souhaitée exprimée en nombre d'UM. Le temps cumulé (en UM), au bout duquel le bout de la lame A passe au-dessus d'un point donné x, est donné par la fonction Ma(x). De même, la fonction Mb(x) nous donne le temps cumulé (en UM) au bout duquel le bout de la lame B passe au-dessus du point x (figure 1). Le point x reste couvert par la lame B jusqu'au moment tb = Mb(x); puis il reste exposé jusqu'au moment tA = Ma(x) où la lame A le recouvre. A partir de ce moment, jusqu'à la fin de l'irradiation, le point x reste couvert par la lame A. La "fluence" totale (exprimée en nombre d'UM) en chacun des N points x choisis sur l'axe x est alors:
F(xi) = Ma(xi) - Mb(xi), i = l...N [eqn.1].

Fig 1. Relation entre la fluence désirée F(x) et les trajectoires de lames Ma(x) et Mb(x) aux points xi et xi+1. En pratique, F(x) est acquise par des donnés numériques et par conséquent elle est discrète. On suppose qu'elle est constituée de segments linéaires.
Les lames ont la possibilité de se déplacer avec des vitesses différentes. L'équation reliant leurs vitesses Va et Vb est:
Va(xi+1) et Vb(xi+1) £ Vmax i=1,…,N-1
Les vitesses Va et Vb sont exprimées en cm/UM. Vmax est la vitesse maximale du déplacement des lames. Elle est obtenue à partir de la vitesse maximale mécanique des lames VMmax (en cm/s) et du débit de dose D (en UM/rnin) supposé constant par la relation :Lorsque le profil F(xi) est connu en tous les points (i = 1,...N), l'équation [1] peut être résolue pour les deux inconnues Va et Vb. Il existe donc une infinité de solutions. Ce degré de liberté supplémentaire est utilisé en posant Vb = Vmax pour les segments croissants du profil (F(xi+1) ³ F(xi)) et Va = Vmax pour les segments décroissants du profil. Ainsi, pour chaque segment, la lame la plus rapide est programmée pour se déplacer avec la vitesse maximale. La vitesse de l'autre lame est définie par l'équation [1].VMmax
V max = -------------
D/60
Il s'ensuit que, puisque l'efficacité pour chacun des segments est maximale, le temps total d'irradiation est minimisé. Cette conclusion est représentée, sous la forme de l'algorithme suivant:
Si F(xi+1)
³ F(x) alors
L'extension de cet algorithme aux autres paires de lames, pour la production d'une modulation d'intensité 2D, nécessite l'application d'une procédure de synchronisation des lames. Dans tous les collimateurs multilames disponibles sur le marché, un arrangement de type "tenon-mortaise" (tongue and groove) est utilisé pour la réduction des fuites entre lames adjacentes. En raison de cet arrangement, des sous-dosages importants peuvent se produire, lors la production de faisceaux d'intensité modulée par collimateur multilames. Ce problème a été traité initialement par Van Santvoort et Heijmen (1996) [32] et étudié plus en détail par Webb et al [37]. Il est schématisé sur la figure 2.
Si les lames ja, jb, (j+1)a et (j+1)b se déplacent avec la même vitesse constante de gauche à droite, les intensités produites Fj et Fj+1 (pour les points totalement exposés) sont égales aux intensités prescrites. En revanche, dans la région de superposition de deux paires de lames adjacentes, l'intensité produite Fs est considérablement inférieure à Fj ou Fj+1 Ces points sont découverts seulement pendant la période où la lame b de la paire j est déjà passée et la lame a de la paire j+1 n'est pas encore arrivée. En synchronisation (de la paire j+1 avec la paire j), les lames de la paire j+l (la paire la plus avancée) sont recalées de telle façon que l'intensité délivrée dans la région de superposition soit égale à l'intensité Fj+1. Ainsi, le problème d'un sous-dosage dans la région de superposition est évité.
En raison de son principe (ralentir afin de synchroniser) l'application de la synchronisation est toujours caractérisée par un temps d'irradiation supérieur ou égal à celui d'une méthode non-synchronisée. Selon Van Santvoort et Heijmen [32], cette augmentation est de l'ordre de 5 à 15 %.
Les algorithmes décrits précédemment ont été intégrés dans un logiciel spécifique conformément au schéma de la figure 3.
La distribution d'intensité incidente désirée qui constitue l'entrée du programme est exprimée sous forme d'une matrice contenant les coordonnées (x, y) de chaque point et le nombre d'UM à délivrer en ce point. Les positions des lames et le temps total d'irradiation (le nombre total d'UM pour effectuer l'irradiation dynamique) calculés par le logiciel sont structurés sous la forme d'un fichier compatible avec l'ordinateur de contrôle des lames2 Ce fichier est ensuite transféré à l'appareil de traitement pour commander le déplacement des lames.
2 Varian MLC Controler software.

Fig 2. Synchronisation des lames. Seules deux paires de lames sont montrées. Toutes les lames se déplacent avec la même vitesse constante de gauche à droite (les flèches indiquent la direction du déplacement). a. En raison de l'arrangement tongue and groove entre les deux paires de lames, les points de la région de superposition F, sont toujours sous l'une ou l'autre des lames j et j+1. La fluence dans cette région est donc nettement inférieure à celle délivrée dans les régions totalement exposées (Fj et Fj+1). b. Avec synchronisation. les lames de la paire j+1 (la paire la plus avancée) sont recalées de telle façon que l'intensité définie dans la région de superposition Soit égale à l'intensité Fj+1. Ainsi, le sous-dosage dans la région de superposition est évité tout en donnant la même distribution de fluence dans les régions Fj et Fj+1 [32].
Procédure expérimentale
Dans le cadre de notre étude de faisabilité et n'ayant pas encore pu disposer du logiciel de contrôle dynamique des lames, nous avons testé l'efficacité de notre programme en simulant une irradiation dynamique par une séquence d'irradiations statiques. Cette approche avait été proposée comme méthode de traitement par plusieurs auteurs [3, 14, 16]. Pour produire le champ d'intensité modulée, le logiciel a donc calculé la position des lames à plusieurs instants successifs.
Les lames sont placées conformément au premier champ statique puis le faisceau est lancé jusqu'à ce qu'un nombre spécifié d'UM soit délivré. Pendant le repositionnement des lames, le faisceau est arrêté. La procédure continue et chaque fois l'accélérateur délivre la quantité d'UM spécifiées.
L'approximation de la distribution d'intensité sera d'autant meilleure que l'intervalle de temps (en UM) correspondant à chaque positionnement des lames sera petit. E est évident que, pour un temps total d'irradiation donné (calculé par notre programme et exprimé en UM), il est souhaitable d'utiliser un grand nombre de pas dans la séquence d'irradiations.
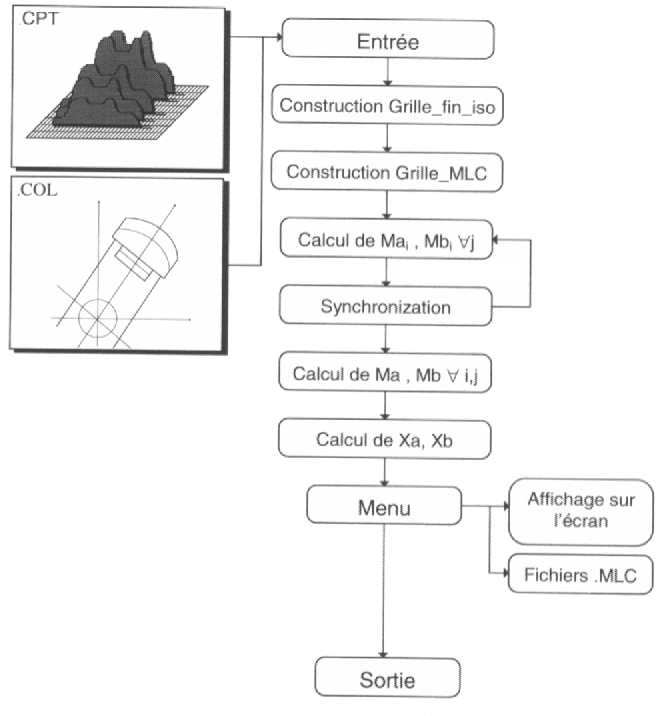
Fig 3. Organigramme du logiciel développé. permettant le calcul de la relation entre position de lames et nombre d'UM. Les données d'entrée Sont deux fichiers CPT et COL correspondant à la modulation d'intensité désirée et aux caractéristiques du collimateur multilames respectivement. Après transcription des données dans une grille adaptée, le calcul des positions des lames est effectué. Les résultats sont stockés dans un fichier MLC (collimateur multilames) compatible avec la console qui contrôle les lames.Cependant, l'administration consécutive de très faibles quantités d'UM risque d'introduire des imprécisions importantes. Nous avons choisi de ne pas utiliser une quantité d'UM par pas inférieure à 5 UM.
Pendant l'irradiation, les mâchoires du collimateur principal ont été positionnées à l'extérieur du champ carré ou rectangulaire qui encadre la région totale à irradier. En pratique. des dimensions de champs de l'ordre de 10 x 10 cm ont été utilisées. Des marges de 0,2 cm dans la direction Y et 0,4 cm dans la direction X (direction du déplacement des lames) ont été appliquées par rapport aux lames les plus écartées, afin que la pénombre ne soit formée que par les lames et non par les mâchoires.
Des films (AGFA Structurix) ont été utilisés pour intégrer la dose délivrée par le système de collimation dynamique. Les films ont été placés à la profondeur du maximum (dmax) dans un fantôme homogène de polystyrène. perpendiculairement à l'axe du faisceau. La distance source-film a été égale à 100 cm.
Modu1ation d'intensité pur collimateur multilames. L'énergie du faisceau utilisé à été de 6 MV. Les conditions d'irradiation des films sont précisées sur la figure 4.
Pour les deux exemples de champs d'intensité modulée présentés dans cet article, le maximum de l'intensité désirée exprimée en nombre d'UM a été égal à 80. Pour rester dans la région linéaire de la réponse du film tout en gardant un nombre de pas important, nous avons interposé dans le faisceau un atténuateur, constitué d'une plaque de laiton de 2,11 cm d'épaisseur (transmission de 0,497), placée sur le porte-caches (figure 4). Ainsi, pour les conditions d'irradiation données la dose maximale intégrée par les films était de l'ordre de 40 cGy. D'après une courbe d'étalonnage prédéterminée pour ce type de films, cette dose maximale reste dans la région de linéarité de la réponse du film. La variation de la densité optique du film après l'irradiation est donc proportionnelle à la variation de la dose.
Les films ont été développés manuellement. Pour la lecture de la densité optique de chaque film, un système contrôlé par ordinateur dont la résolution spatiale était égale à 0,5 mm a été utilisé (Wellhôfer 2D densitometer). Une traversée a été mesurée le long de chaque paire de lames. Les profils de densité optique qui en résultent n'ont pas été convertis en dose et la comparaison entre les données désirées et mesurées qui suit, est qualitative. Les irradiations des films constituent une première approche afin de montrer le potentiel de la méthode.
RÉSULTATS
Modulation 1D
Afin d'illustrer les principes de l'algorithme, nous présentons le calcul des trajectoires des lames (calcul sans mesures) pour deux exemples de profils d'intensité modulée (figures 5 et 6). Le premier est un profil simple et linéaire en coin. Le second est un profil arbitraire.
Dans la figure 5a la pente du profil à produire est constante et égale à 4 UM/cm. Une vitesse critique est définie par l'inverse de cette pente. Si la vitesse maximale autorisée est supérieure à cette vitesse critique (ie Si Vmax > 0,25 cm/UM), le profil peut se produire par le mouvement d'une seule lame. Sinon, les deux lames sont nécessaires. Ces deux cas sont illustrés dans la figure 5. Avec une vitesse maximale Vmax = 0,4 cm/UM, la condition est satisfaite et la lame b reste immobile à la position x = +5 cm, tandis que la lame a, seule, produit le profil désiré (figures 5b1 et 5e1). En revanche, avec une vitesse maximale de 0,2 cm/UM, inférieure à la vitesse critique, les deux lames sont employées pour la production du profil désiré (figures 5b2 et 5c2). Le temps total de l'irradiation (Ttot), pour Vmax supérieure à la vitesse critique, est Ttot = 90 UM qui est égal à la valeur maximale du profil à produire. Pour des valeurs de Vmax inférieures à la vitesse critique, le temps total d'irradiation augmente. Avec une vitesse maximale Vmax = 0,2 cm/UM, le temps total d'irradiation est 140 UM.

Dans la figure 6, le profil à produire a une forme arbitraire. Les deux lames se trouvent initialement à la même position et commencent à se déplacer vers le bout opposé du profil avec des vitesses variables. La séparation entre les lames à chaque instant est également variable. Pour un segment croissant du profil, la vitesse de la lame b est supérieure à la vitesse de la lame a et vice-versa. La lame b arrive en premier au bout du profil pour t = 30 UM et y reste jusqu'à la fin de l'irradiation. La lame a suit et arrive à la même position pour t = 110 UM (figure 6c). Le temps total d'irradiation est alors 110 UM. La valeur maximale du profil désiré est égale à 80 UM. Pour un profil donné, les trajectoires des lames sont définies par la vitesse maximale mécanique des lames. Le temps total d'irradiation exprimé en UM est inversement lié à Vmax.Fig 4. Conditions d'irradiation des films: La distance source-film est de 100cm. Le film est placé perpendiculairement à l'axe du faisceau, à la profondeur dmax, dans un fantôme homogène de polystyrène. Une énergie de 6 MV est utilisée. Un atténuateur, constitué d'une plaque de laiton de 2,11 cm d'épaisseur (transmission de 0,497), est placé sur le porte-caches.
Modulation 2D
Les fichiers contenant les positions des lames pour chaque sous-champ dans la séquence d'irradiation ont
été préparés par notre application et stockés sur l'ordinateur qui contrôle le déplacement des lames. Afin de délivrer la séquence, le fichier correspondant au champ modulé est chargé en mémoire et ensuite exécuté. Dans la séquence d'irradiations, l'ensemble des positions des lames forme une ouverture (fenêtre) qui se déplace à travers le champ (figure 7). Deux exemples sont décrits ici.
Fig 5. Application de la technique itérative sur un profil en coin (a). Les trajectoires de lames, exprimées à la fois en fonction de la position (b) et en fonction du temps (c), sont calculées pour deux valeurs différentes de la vitesse maximale de déplacement des lames (indices 1 et 2). On remarque que pour Vmax = 0,4 crn/UM, la lame a seule peut produire le profil désiré tandis que pour Vmax = 0,2 cm/UM, les deux
lames sont employées pour la production du profil.

Dans le premier cas, il s'agit d'obtenir une variation d'intensité linéaire en deux dimensions, selon la diagonale d'un champ 10 cm x 10 cm. La forme de l'intensité désirée est représentée sur la figure 8a1. Les trajectoires des lames ont été calculées par notre programme, ainsi que le temps total d'irradiation trouvé à 130 UM. L'irradiation dynamique a été approchée par une séquence de 26 irradiations de 5 UM chacune. Dix lames (N0 16 à 25) ont participé à la modulation d'intensité.Fig 6. a. Profil d'intensité désiré arbitraire. b. Le temps cumulé (en UM) au bout duquel le bout de chaque lame passe au-dessus d'un point donné x. Lame a: trait en pointillés lame b trait plein. c. Positions des lames en fonction des UM.
La figure 8a1 montre l'intensité (fluence dans l'air en UM) souhaitée, normalisée sur l'axe du faisceau au point x = 0 cm y = 0 cm. La figure 8b1 montre la densité optique du film mesurée et normalisée au même point. La densité optique peut être considérée comme proportionnelle à la dose déposée à dmax, car on est resté dans la région linéaire de la réponse du film. La figure 8c1 montre la comparaison entre l'intensité relative désirée et la densité optique relative mesurée le long de la 20e lame, c'est-à-dire au centre du champ.
On observe un bon accord entre les valeurs souhaitées et les mesures, avec toutefois un "arrondi" en début et en fin de courbe expérimentale. Plusieurs commentaires s'imposent:
- la méthode MLC dynamique ne permet pas toujours de réaliser strictement ce qui est souhaité. Sur la figure 8c1, on observe en particulier que la partie de la courbe caractérisée par des valeurs nulles n'est pas correctement reproduite. Les différences observées s'expliquent par le fait que la transmission au travers des lames, la pénombre, et la diffusion par le collimateur de la machine interviennent dans les mesures alors qu'ils avaient été négligés dans le calcul de la position des lames;
- de plus, le dispositif expérimental est source de "lissage": le film a été positionné à dmax et les photons diffusés par le milieu interviennent dans les données mesurées. L'utilisation de la plaque de laiton est également à mettre en cause dans le processus de lissage expérimentai de la courbe. D'ailleurs, dans le cadre de cette étude de faisabilité, en réalisant l'approximation du mouvement continu par des positions discrètes de lames, on s'attend à obtenir des marches d'escalier mais le "lissage" expérimental atténue l'effet attendu.
Dans le second cas, nous avons déterminé la modulation d'intensité nécessaire pour compenser les irrégularités de surface (dans la région du cou) d'un vrai patient. Cette modulation d'intensité a été préparée par un système de calcul des doses qui effectue le calcul des épaisseurs d'un compensateur-photons conventionnel3. Le temps total d'irradiation, tel qu'il a été calculé par notre programme, était de 110 UM. L'irradiation dynamique a été approchée par une séquence de 22 irradiations de 5 UM chacune. La figure 8a2 montre l'intensité (fluence dans l'air en UM) souhaitée, normalisée sur l'axe du faisceau. La figure 8b2 montre la densité optique relative d'un film qui a été placé à la profondeur dmax, normalisée également sur l'axe du faisceau. Dans la figure 8c2 on observe la densité optique relative mesurée comparée à l'intensité relative désirée pour la vingtième lame. Une fois de plus, et pour les mêmes raisons, un lissage de la courbe apparaît, mais l'accord entre les deux courbes n'est pas mauvais compte tenu de notre approximation de premier ordre.
3 Système ISIS Institut Curie/Technologie Diffusion.
Fig 7. L'ensemble des lames à chaque instant forme une fenêtre qui se déplace dans le champ.

Fig 8 a. Deux exemples (indices 1 et 2) de faisceaux modulés en intensité sur deux dimensions. a. Intensité relative désirée (normalisée à l'axe du faisceau). b. Densité optique relative mesurée (normalisée à l'axe du faisceau). c. Comparaison entre l'intensité relative désirée (trait plein) et la densité optique relative mesurée (trait en pointillés) le long de la 20' lame.
CONCLUSION
Des outils logiciels ont été mis au point pour convertir une fluence souhaitée en mouvement de lames. Ces outils ont fait l'objet d'une validation à la fois théorique et expérimentale et les résultats sont satisfaisants.
L'analyse des résultats démontre la possibilité d'appliquer une collimation dynamique en utilisant le collimateur multilames afin de créer des champs d'intensité modulée. La procédure est générale et peut être employée lorsque le volume cible n'est pas trop large par rapport à la zone couverte par le déplacement des lames. La méthode peut être appliquée dans tous les cas nécessitant une modulation d'intensité. Bien que notre approche néglige certains phénomènes liés aux caractéristiques physiques du faisceau de photons, nous avons obtenu un bon accord entre la distribution de dose souhaitée et celle obtenue sur la machine de traitement équipée du collimateur multilames. Pour répondre aux exigences de la modulation d'intensité, celui-ci doit comporter un grand nombre de lames, de faible largeur au niveau de l'isocentre, et ayant la capacité de dépasser largement l'axe du collimateur. En effet, d'une part, la résolution spatiale de la modulation produite est d'autant plus élevée que le nombre de lames est grand et que leur largeur au niveau de l'isocentre est faible et d'autre part, avec la technique de la fenêtre glissante, comme les lames opposées démarrent du même côté du champ et se déplacent vers l'autre côté, les dimensions maximales du champ modulé sont d'autant plus importantes que la capacité de dépasser l'axe du collimateur est grande. Pour une irradiation complètement dynamique, les lames doivent également avoir la possibilité de se déplacer pendant l'irradiation avec des vitesses variables.
Il reste à appliquer notre logiciel à une collimation véritablement dynamique qui est maintenant disponible sur l'accélérateur que nous avons utilisé et à prendre en compte certains phénomènes négligés jusqu'à présent. La prise en compte des caractéristiques mécaniques et physiques du collimateur multilames (accélération/décélération, pénombre, transmission, fuites, etc), est nécessaire pour le calcul de la dose. Il faut de plus mettre au point les méthodes dosimétriques adaptées à ce mode de fonctionnement et définir une procédure de contrôle de qualité, avant de pouvoir réaliser une utilisation dynamique clinique du collimateur multilames.
REMERCIEMENTS
Les auteurs tiennent à remercier MC Murillo et H Szymanowski, pour leurs conseils et leur collaboration, ainsi que professeur C Kappas pour les entretiens fructueux que nous avons eu avec lui. Nous adressons également nos remerciements à Varian Médical - France.
RÉFÉRENCES
- Barth NH. An inverse problem in radiation therapy. Int J Radiat Oncol Biol Phys 1990; 18 : 425-31
- Bonfeld T, Btrkelbach J, Boesecke R, Schlegel W. Methods of image reconstruction from projections applied to conformaI radiotherapy. Phys Med Biol 199035 :1423-34
- Bortfeld T, Kahier D, Waldron T, Bayer A. X-ray field compensation with multileaf collimators. Int J Radiat Oncol Biol Phys 1994 28 : 723-30
- Bayer A, Desobry 0E, Wells N. Potential and limitations of invariant kernel conformaI therapy. Med Phys 1991; 18
- Bayer A, Nyerick C, Ochran T G. Field margin characteristics of a multileafcollimator. Med Phys 1991; 18:606
- Brahme A. Design principles and elinical possibilities with a new generation of radiation therapy equipment [reviewj Acta Oncol 1987; 26:403-12
- Brahme A. Optimization of stationary and moving beam radiation therapy techniques. Radiother Oncol 1981; 12 :129-40
- Brahme A, Roos JE, Lax 1. Solution of an integral equation in rotaton therapy. Phys Med Biol 1982; 27:1221-9
- Castellanos ME, Rosenwald JC. Evaluation of the scatter field for high-energy photon beam attenuators. Phys Med Biol 1998 ; 43 277-90
- Chui CS, LoSasso T, Spiroti S. Dose calculation for photon beams with intensity modulation generated by dynamic jaw or multileaf collimators. MedPhys 1994; 21: 1237-44
- Convery D, Rosenbloom M. The generation of intensity modulated fields for conforma! radiotherapy by dynamic multileaf collimation. Phys Med Biol 1992 ; 37:1359-74
- Cormack A. A problem in rotation therapy with X-rays. Int J Radiat Oncol Biol Phys 1987; 13 : 623-30
- Cormack AM, Cormack RA. A problem in rotation therapy with X-rays: dose distributions with an axis of symmetry.int J Radiat OncoiBiaiphys 1987; 13:1921-5
- Galvin JM, Chen X-G, Smith RM. Combining multileaf fields to modulate fluence distributions. Int J Radiat Oncol Biol Phys 1993 27 : 697-705
- Galvin JM, Smith AR, Lally B. Characterization of a multileaf collimator system. Int J Radiat Oncol Biol Phys 1993 ; 25 :181-92
- Geis P, Bayer A, Welîs N. Use of multileaf collimator as a dynamic missing-tissue compensator. Med Phys 1996; 23 :1199-205
- Gustafsson A, Lind BK, Svensson R, Brahme A. Simultaneous optimization of dynamic multileaf collimation and scanning pattems or compensation fliters using a generalized pencil beam algorithm. Med Phys 1995; 22:1141-56
- Källman P, Lind B, Eklöf A, Brahme A. Shaping of arbitrary dose distributions by dynamic multileaf collimation. Phys Med Biol 1988; 33:1291-300
- Kijewski PK, Chin LM, Bjärngard BE. Wedge shaped dose distributions by computer-controlled collimator motion. Med Phys 1978; S
- Leavin DD, Martin M, Moeller JR, Lee WL. Dynamic wedge field techniques through computer-controlled collimator motion and dose delivery. Med Phys 1990; 17:87-91
- Lind B, Brahme A. Generation of desired dose distributions with scanned elementary beams by deconvolution method. int J Jmaging Sysrems Technol