Application of the LQ model to the interpretation of absorbed dose distribution in the daily practice of radiotherapy

Pierre Scalliet¹ , Jean-Marc Cosset²  and Andre Wambersie^3
1Department of Radiotherapy, AZ Middelheim, Lindendreef Antwero, Belgium,
²Department of Radiotherapy, Institut Gustave Roussy. France.
³Unite de Radiothérapie. neutron- et curiethérapie. Cliniques Universitaires Saint Luc. Bruxelles. Belgium

(Received 2 January 1991, revision received 8 July 1991, accepted 5 August 1991)

 Key words: Linear quadratic model; Computer dosimetry

 Summary

 In 1991, the vast majority of radiotherapy centers are implemented with computer treatment planning systems (TPS), and it has become routine practice to compute fusil absorbed dose distribution (ADD) in almost ail treatment situations. Usually the target is covered by the 100% isodose and the surrounding normal tissues receive a lesser dose than the tumor. It implies, that, as the dose per fraction of, say, 2 Gy is prescribed at the 100%, normal tissues receive a daily dose different than 2 Gy. The absorbed doses delivered at different organs have therefore not the same biological effectiveness and must be corrected according to the actual dose per fraction for a proper interpretation of the treatment planning. This is of great importance since most of the "tolerance levels" used in the practice have been determined for doses per fraction around 1.8-2 Gy. The linear-quadratic (LQ) model provides a simple method for establishing biological equivalencies and has been used throughout this article to establish the difference between the absorbed dose computed by the TPS and its biological equivalent. It is shown that normal tissues receiving less than 100% of the daily dose are relatively more protected than suggested by the ADD, and, inversely, that normal structures overdosed and thus receiving more than the 10000 daily dose are relatively more at risk for complications than suggested from the ADD.

 Introduction

 In 1991, the vast majority of radiotherapy centers are implemented with computer treatment planning sys­tems (TP S), and it has become routine practice to com­pute full absorbed dose distribution (ADD) in almost ail treatment situations. The results are usually dis­played on a cathodic screen or, most often, on paper charts, which serve as a basis for dose prescription. Concentric isodose curves are obtained, labeled according to a reference point usually referred to as the 100% of dose.
However, more than simply calculating ADD from simulation charts, TPS have proven to be valuable tools for dose distribution optimization, i.e. for the definition of optimal beam arrangements, uniformly covering the tumor volume with an adequate absorbed dose, and sparing the surrounding normal tissues as much as possible. In an optimal treatment, sensitive normal structures outside the target volume are irradiated at smaller doses than the tumor, which implies that they are irradiated each day at a smaller dose per fraction than the reference fraction size at the tumor level. This otherwise obvious statement is of basic importance, since the biological effect of any given total dose, in any tissue, depends in first instance on the dose per fraction [1,9]. The classical dose levels of normal tissue toler­ance, only valid at the level of 1.8-2 Gy per fraction [19], can not be applied in absorbed dose optimization procedures, but must be interpreted according to the actual dose per fraction delivered on each session. A further step would compute "isoeffect" i.e. to weight, at each point of interest, the absorbed dose by a weighting factor which takes into account relevant parameters such as the fraction size and the overall time.
Let us illustrate this with some situation where a normal structure, close to the tumor, receives 50 % of the total dose (i.e. lies on the 50% isodose). In such a case, the absorbed dose delivered to this structure is given in the same number of fractions as the 100 % dose delivered to the tumor. Each fraction is then only 50 % of the prescribed fraction size (e.g. 1 vs. 2 Gy), and has a different biological effectiveness. Therefore, the absorbed 50% dose (AD) needs to be translated into a biological equivalent dose (BED), which takes into account the actual dose per fraction and the radio­biological characteristics of the relevant tissue. This is of particular importance in daily clinical applications since, as mentioned before, most of the maximal tolerance doses used in our common practice are assumed to be delivered in fractions of 2 Gy.
From a mathematical point of view, the problem is simple. But the real question is the validity of the biological concept involved. In the past, the NSD has been proposed for the calculation of isoeffect doses [8]. The practice has soon proved its limitations, especially in the calculation of dose equivalencies of treatments delivered with a number of large fractions to late responding tissues. Attempts to replace the classical fraction of 2 Gy by larger fractions (2.5 or 3.3 Gy) eventually led to catastrophic normal tissue late dam­ages [5]. The NSD should undoubtedly no longer be used.
In the past 10 years, the linear-quadratic (LQ) model has gained general acceptance as a comprehensive and biologically more founded isoeffect model, supported by a large number of clinical and radiobiological publi­cations (extensively reviewed by Thames and Hendry [24]).
This paper deals with the use of the LQ isoeffect model in the interpretation of ADD, and more particu­larly in the calculation of isoeffect (or biologically equivalent) doses, in normal tissues receiving a dose different to the 100% prescribed dose.

 Materials and methods

 Patient data

 The following examples have been based on thoracic CT images. Indeed, thoracic tumors often challenge the ability of radiotherapy to deliver tumoricidal doses, without exceeding normal tissue tolerance. In example 1 and 2, the CT plane passes through a theoretical mediastinal tumor, located 1 to 2 vertebral bodies below the carina. It may correspond, for instance, to an oesophageal cancer or to a bulk of adenopathies of various origin. The spinal cord, the heart and the lungs are the normal, dose limiting, tissues, extending over the whole height of the tumor. The heart is actually below the central plane but is included in the lower half of the field. The actual CT body cross-section was obtained in a 54-year-old man suffering from a squamous cell car­cinoma of the oesophagus (level Th 8).

Example 3 is based on an other CT cross-section through the thorax of a 64-year-old man treated for a non-small-cell bronchial carcinoma of the right lung (level Th 6).

Physical parameters

 The ADD was computed with a SIDOS 1.1.6 system (Siemens) running on a PDP 11/35 computer (Digital). The contour and tumor location were acquired by CT scan thoracic cross-sections (Tomoscan, Siemens), and entered in the computer with a digitalizer. The cor­rection for heterogeneities were made assuming a den­sity of 1.16 for bone and 0.33 for lungs.

 In the third example, a mixed photon/neutron schedule is presented. The dose was expressed in terms of "photon equivalent dose" using a clinical RBE of 2.8 for neutrons (see below). The neutron dose distribution was based on depth-dose curves measured in a water phantom with the p(65) + Be neutron beam of Cyclone, Louvain-la-Neuve, and the correction for heterogene­ities was tentatively based on the same density factors than for photons. No correction was attempted for heterogeneities in tissue hydrogen content.

 In example 1, the beam arrangement was chosen to optimize dose distribution throughout the target vol­ume, using 18 MV photon isocentric fields produced by a linac (Saturne CGR). The solution was found satis­factory for a 54 Gy prescribed dose, with a limited dose to the surrounding normal tissues. This dose of 54 Gy was specified according to ICRU 29 [13] recommenda­tions (at intersection of beam axes). However, this example does not constitute any recommendation for the treatment of mediastinal tumors since other field arrangements are certainly equally good.

 In example 2, the same contour, without the tumor, has been used to discuss the problem of one-field-per ­day treatments with various photon energies: 18 MV photons vs. cobalt-60 gamma rays (Gammatron S Siemens).

 Example 3 was computed for mixed beams of 18 MV photons (lateral fields) and p(65) + Be neutrons (AP fields). The depth dose distribution of p(65) + Be neutrons is similar to the one obtained with 8 MV pho­tons. The characteristics of this beam have been described elsewhere [28].

 Isoeffect formulas

 While the effect of fractionation has been recognized a long time ago [6-8,18], it is only recently that isoeffect models included specifically this parameter in the calculation of treatment equivalencies.

This finding has logically lead to the definition of new isoeffect relationships, the most recent of which being based on the LQ ceil survival model [4,15]. This model is at present considered to be the most reliable one, mainly for two reasons: its ability to describe adequately the variation of isoeffect dose with the fraction size within a dose range of interest to the clinic (1-1.5 to 9-10 Gy), and its great simplicity of use in the daily radiotherapy routine. Extensive discussions concerning the relevance of this formalism have been published, to which the reader can refer for a basic understanding of the mathematical equations (see refs. [9,24]).

It has been shown that the influence of fractionation on a variety of normal tissues can be described on the basis of a simple formula relating the radiation effect (E) to the total dose (D) delivered in (n) fractions of size (d): the LQ dose effect relationship:

 E = a (nd) + b (nd)² = aD + bDd

From this equation, the ratio a /b is derived as an essen­tial parameter for the description of fractionation effects. a and b are constants with specific values depending on the measured effect (i.e. the tissue involved) and on the irradiation conditions (radiation quality, dose rate...).

Calculation of isoeffect dose equivalencies when altering the fraction size can be done very simply, by using the formula developed by Withers [29]:

 (see Appendix)

Where D is a reference total dose delivered at a given fraction size d and D' the unknown total dose delivered at a new fraction size d'. This can be illustrated with a short example. Let us consider a classical treatment of 60 Gy (D) in 30 fractions of size 2 Gy (d), to be replaced by a new schedule with 3 Gy per fraction (d'). To find the new total dose D', isoeffective to 60 Gy in 30 fractions, we may write:

To solve the equation, a choice of an a /b value must be made. We already know, from radiobiological as well as from clinical data (recently reviewed in [9] and [25]), that normal tissue reactions are broadly distributed into two categories: the early reacting tissues, characterized by low fractionation sensitivity, and the late reacting tissues with large fractionation sensitivity. An a /b value of 10 Gy is usually attributed to the former, and a value of 2 to 3 Gy to the latter. It has been shown elsewhere [1,9] that these two values are sufficiently representa­tive of the two groups of tissue reactions and that the error is small when one uses average a /b value in place of the exact one derived from experimental work (in fact, each tissue seems to have its own a /b; see further). We may thus carry on with our formula, and calculate for both types of tissue reactions:

  for a /b = 2Gy

 for a /b = 10Gy

which gives D' = 48 Gy and D' = 55.4 Gy, respectively. Thus, according to Wither's LQ isoeffect equation, 60 Gy in 30 fractions is equivalent to 48 Gy in 16 fractions (48 divided by 3 Gy, the new dose per fraction), for a tissue with a /b = 2 Gy; for a /b = 10 Gy, the equivalent to 60 Gy is 55.4 Gy, which corresponds to something comprised between 18 and 19 fractions of 3 Gy (exactly 18.4, but one has to choose...).

It is now clear that, apart the fraction size, the all important parameter is the ratio a /b. On the basis of these considerations, it becomes clear that fraction size alterations, for doses of interest in radiation therapy, will result in a larger tolerance dose variations in late than in early reacting tissues. Indeed, in our example, late reacting tissues need a dose reduction of 20% whereas early reacting ones need only 8% of dose reduction when increasing the dose per fraction from 2 to 3 Gy.

This equation has been used throughout the follow­ing examples for the calculation of BED from ADD provided by the TPS. Before starting with the examples, a last remark seems necessary: ample evidence exists that doses per fraction larger than 2 Gy can lead to severe clinical problems in late reacting tissues if the proper dose reduction factor is not applied. On the other hand, a reduction of the dose per fraction below 2 Gy is expected to allow for an increase in total dose, but this is far less demonstrated in the clinic than it has been in experimental radiobiology. More clinical data are needed before extrapolating with full confidence from radiobiology to radiotherapy. Some answers have been found in the Institut Gustave Roussy experience of lung irradiation in Hodgkin's tumors (unpublished results). Between January 1988 and December 1989, 25 patients have been irradiated with lung attenuator blocks reducing the daily dose from 2 to 1 Gy. Twenty Gy were delivered to the lungs in 4 weeks with this technique. So far, no toxicity could be detected, either symptomatically or radiologically. Functional evalua­tion was carried out in 7 patients, with all 7 tests within the normal range for age and sex. This suggests that the reduction in dose per fraction actually protects lungs and by extension other late reacting tissues as amply suggested by experimental irradiation in animal models.

 Results and discussion

 Example 1

Figure 1 illustrates the ADD in a transversal section of the thorax (level Th 8), for a theoretical posterior mediastinal tumor. Four perpendicular isocentric fields deliver an homogenous dose throughout the target vol­ume, with an acceptable dose to the surrounding normal structures (heart, spinal cord and lungs). Fifty-four Gy are prescribed on the 100% isodose, and, according to ICRU 29 specified at the intersection of the beam axes. The treatment is planned in 27 daily fractions of 2 Gy. The four fields are to be treated on each day, 5 days per week.

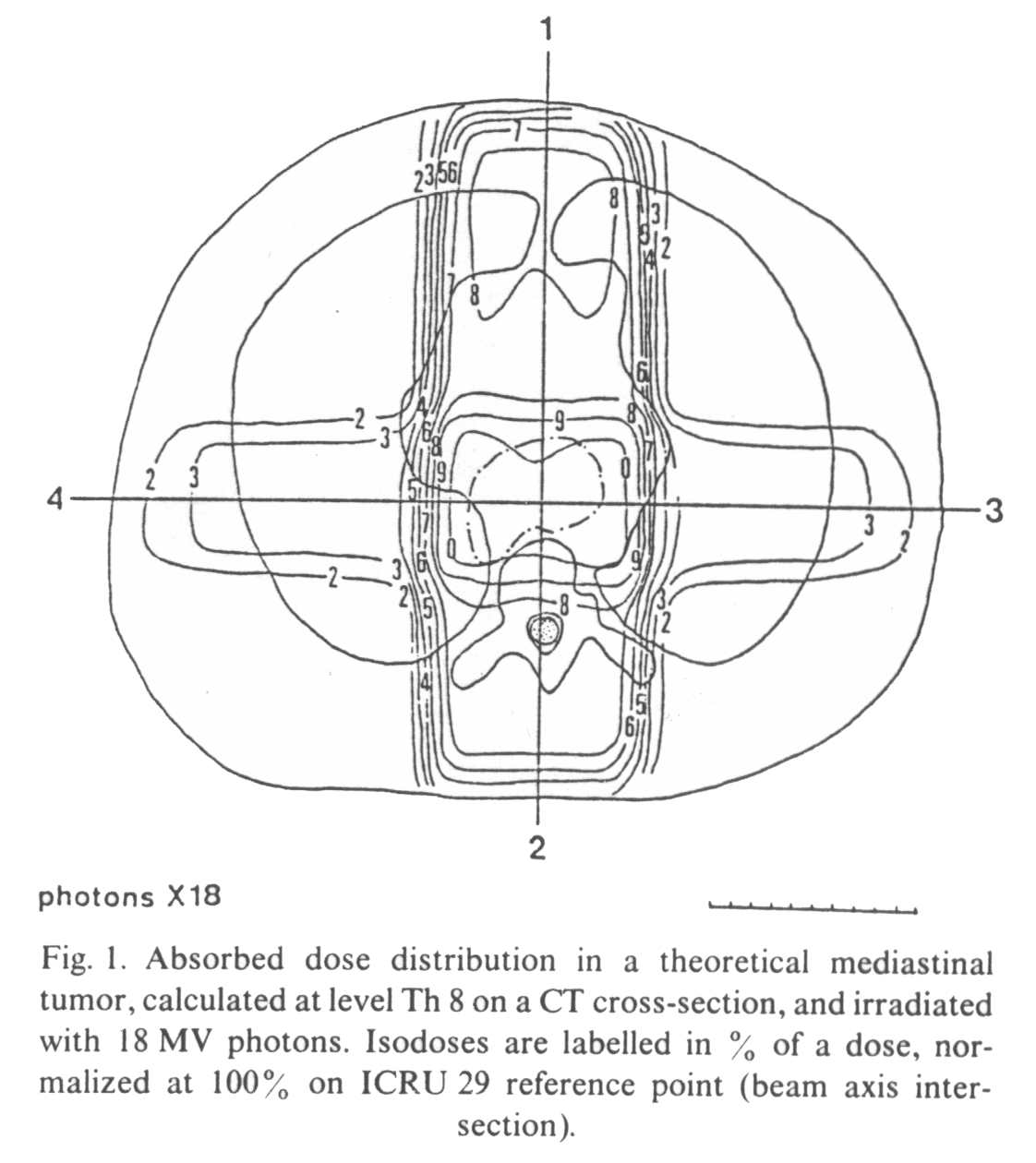
The spinal cord receives 75% of the dose (40.5 Gy) in 27 fractions, i.e. with doses per fraction of 1.5 Gy. Part of the lungs is irradiated by the lateral fields, receiving 30-40% of the dose, i.e.  16.2-21.6 Gy by 27 fractions of 0.6-0.8 Gy. The heart receives on aver­age 80% of the total dose, i.e. 43.2 Gy by fractions of 1.6 Gy.

Assuming a common a /b value of 2 Gy for these (late reacting) tissues, the dose equivalent to a treatment delivered at 2 Gy per fraction can be calculated. The results are given in Table I : 35.4 Gy BED vs. 40.5 Gy AD  for  spinal  cord,  10.5-15.1 Gy  BED  vs. 16.2-21.6 Gy AD for lungs and 38.8 Gy BED vs. 43.2 Gy AD for the heart, respectively.

 If, instead of a generalized a /b value of 2 Gy, we introduce the actual a /b derived for the heart, lungs and spinal cord from radiobiological studies on the fractio­nation effect, we obtain the following results.

 Heart: an extremely low a /b value of 1 Gy was sug­gested by Lauk et al. [16] after selective irradiation of the rat heart (endpoint was lethality form congestive heart failure). The BED recalculated according to this value is 37.4 Gy.

Lung: in a recent publication, Van Rongen et al. [27] quoted a value of 2.3 Gy for late fibrosis of the rat lung (as assessed by measurements of hydroxyproline con­tent of the lung parenchyme 18 months after irradia­tion). With this value, the BEDs become 10.9 and 15.6 Gy, respectively.

Spinal cord: van der Schueren et al. [26] derived an a /b value of 1.7 Gy for the rat spinal cord (measured from hindleg paralysis induction after cervical cord irradiation), which results in the present situation in a BED of 35 Gy.

 The biological equivalent total dose is lower than the absorbed dose in these three tissues, which ensues from their irradiation at a smaller daily dose than the 100% fraction size of 2 Gy. Moreover, the lower the fraction size, the larger the difference between the AD and the BED: 20% difference in the spinal cord, located on the 70% isodose in our dosimetry, vs. 35% in lung, lying on the 30% isodose (a consequence of the important fractionation sensitivity of late reacting tissues around 2 Gy per fraction). It is also shown that the introduction of exact a /b values instead of a common average a /b of 2 Gy for late reacting tissues do not change the situation that much, since the differences in BEDs calculated with both values do not exceed 4%.

According to these calculations, it would be theoretically possible to increase the tumor dose without exceeding the tolerance of normal tissues. If, for example, 60 Gy were delivered to the tumor, the AD to the spinal cord would be closer to the limit that can be safely reached. However, the BED would still remain below the common accepted limit for the irradiation of a large segment of the myelum (something around 45 Gy with 2 Gy per fraction).

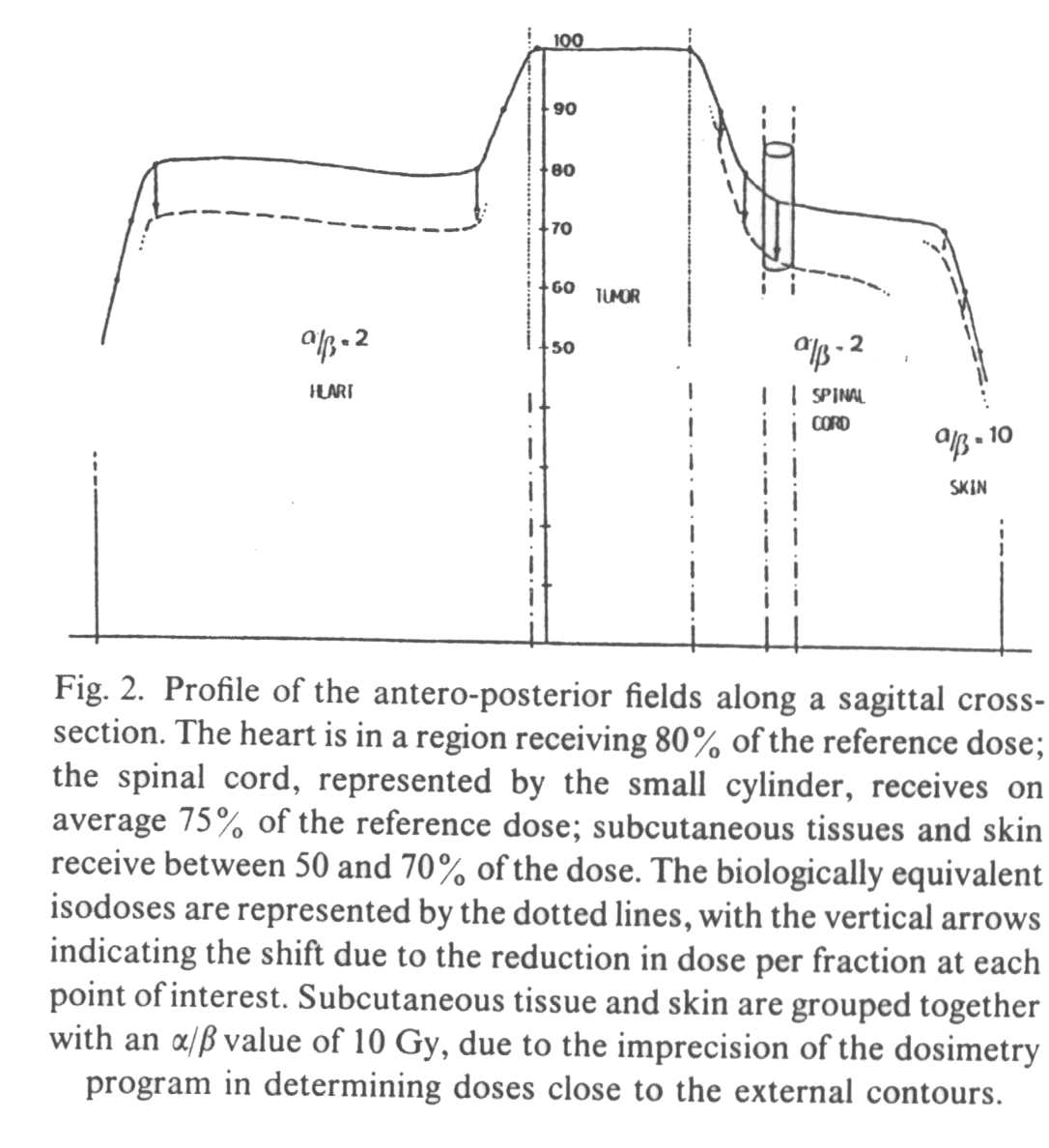
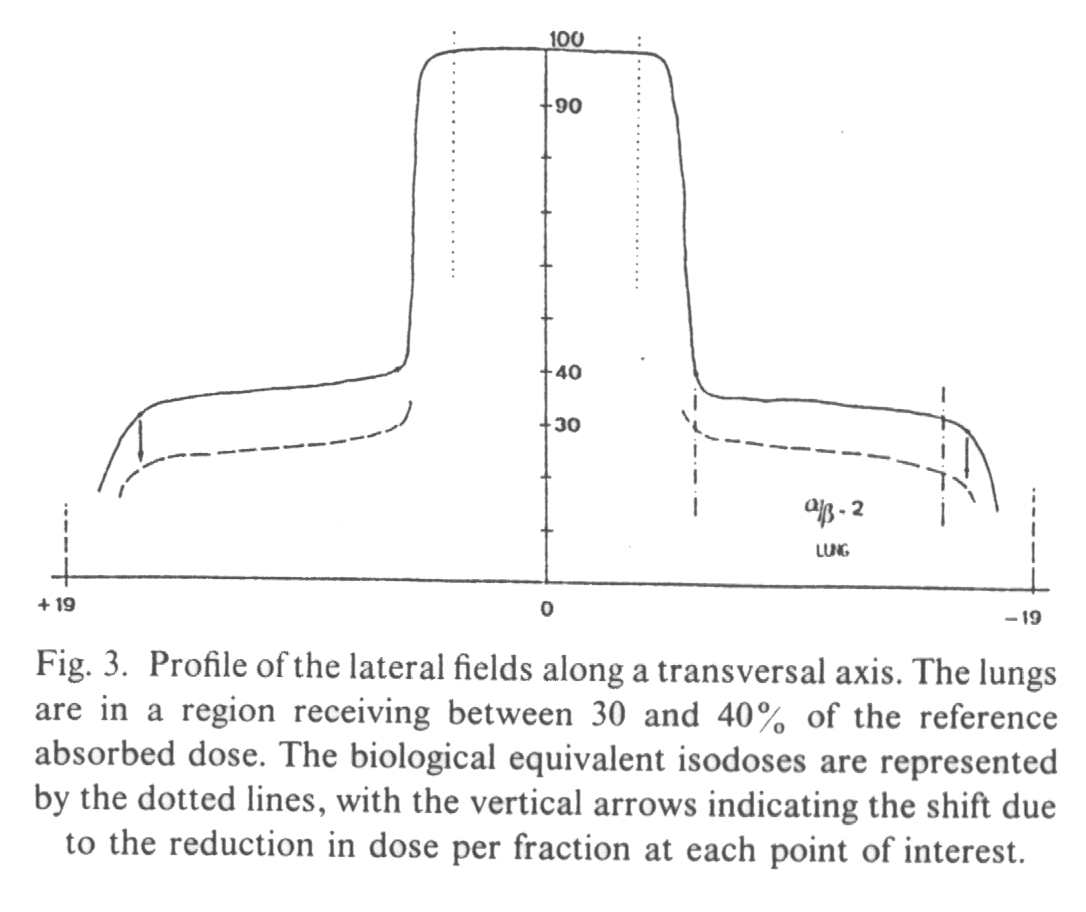
A profile of the anterio-posterior (AP) fields (Fig. 2) and of the lateral fields (Fig. 3) demonstrates that the biological penumbra is more favorable than the simple physical penumbra, in late responding tissues receiving less than the (100%) tumor dose. The 90% isodose becomes the 85% biological isodose, the 80% becomes the 71%, the 75% becomes the 65%, the 40% becomes the 28% and the 30% becomes the 19%.

 With respect to the skin, receiving along the AP axis a dose comprised between 70 and 50% of the tumor dose,  the  same  calculations  performed  with a /b = 10 Gy shows that the difference between BEDs and ADs is much smaller (Table I). This simply reflects the fact that for fraction sizes smaller than 2 Gy, a further decrease in the dose per fraction has but a small influence on the biological effect in early reacting tissues.

 Example 2

The second example is based on dose distribution from two parallel opposed fields in the same thoracic cross-9Mb) section where the tumor contour has been omitted. Calculations are done with two different photon ener­gies, giving the distribution of dose for an anterior, a posterior and two parallel opposed fields, either with cobalt-60 (SSD 80 cm) or with 18 MV photons. Two situations are envisaged: (1) the two fields are irradiated daily and (2) the anterior and the posterior fields are alternatively treated every other day*. Figure 4 shows the different sets of isodoses for cobalt-60 and Fig. 5 for 18 MV X-rays.

 A similar example was developed in Fletcher's Textbook (Fig. 2-9, p. 115, 3rd edn., 1980), but calculated with the single-hit multitarget model, much less easy to handle and to convert in a simple isoeffect formula such as the one proposed by Withers.

If anterior and posterior fields are equally weighted, it is shown that for an AD of 36 Gy at midplane the spinal cord receives 37.8 Gy (105%) with 18 MV photons and 43.2 Gy (120%) with cobalt-60 gamma rays. The superiority of high energy photons speaks for itself, but even with cobalt-60 the dose to the spinal cord seems to remain within tolerance limits.

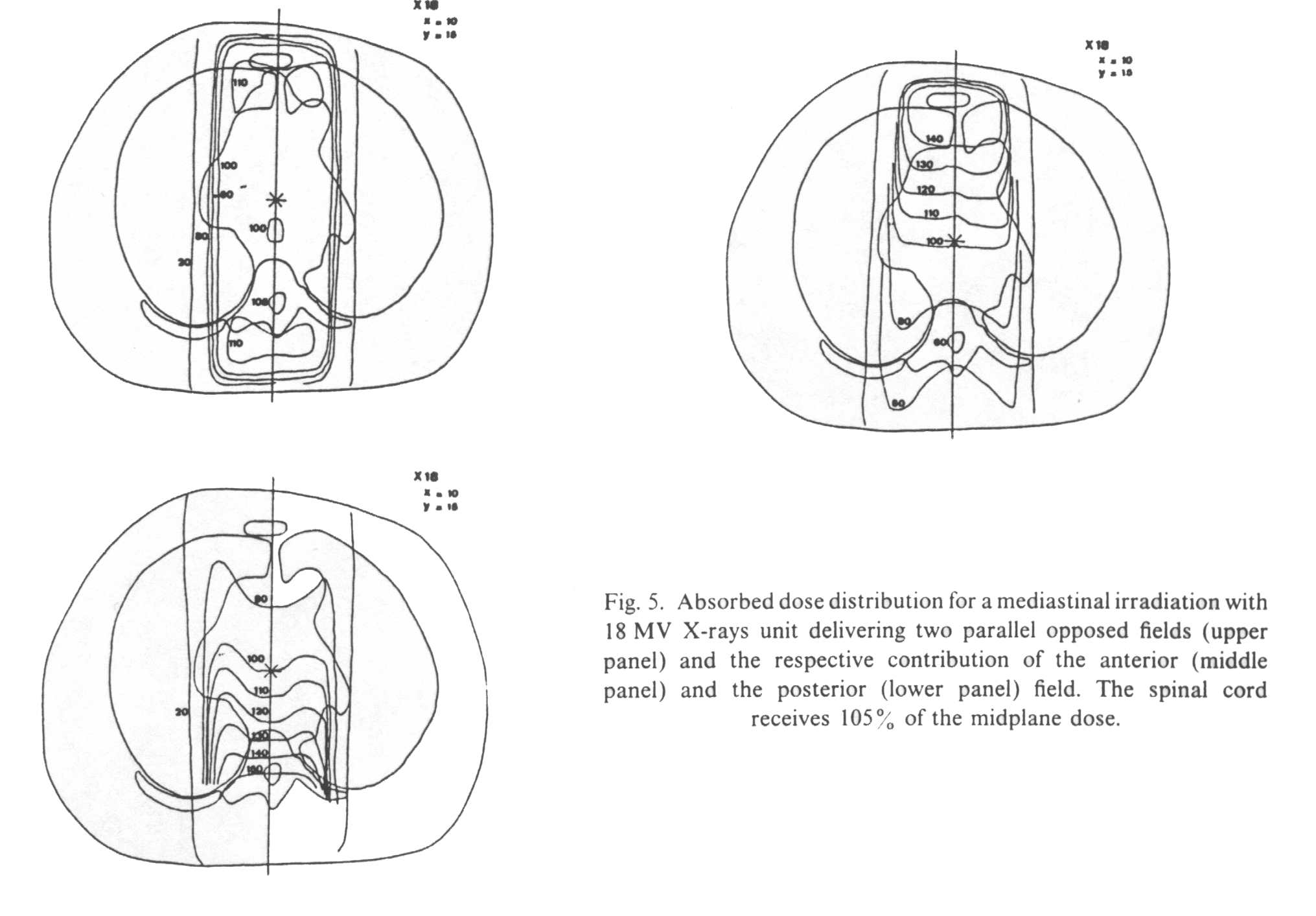
Cobalt-60.  The 36 Gy at midplane are delivered in 18 fractions of 2 Gy, 9 by the anterior and 9 by the posterior field. When irradiating the anterior field, the spinal cord receives 55% of the midplane dose, i.e. 9.9 Gy with a dose per fraction of 1.1 Gy. For the posterior field, the spinal cord receives 182% of the midplane dose, i.e. 33.3 Gy with a fraction size of 3.7 Gy. The total absorbed dose to the spinal cord, taking into account the contribution of both the anterior and the posterior field, is 9.9 + 33.3 = 43.2 Gy (Table II). 

If the two fields are treated on each day, we can reasonably assume that no significant repair takes place during the few minutes necessary for the set-up of the second field after the first has been irradiated. One can consider that the two fields are treated simultaneously with dose per fraction to the spinal cord of :

 (1.1 + 3.7) / 2  = 2.4 Gy    (i.e. 120% of the dose per fraction of 2 Gy at midplane).

 The BED for d = 2.4 Gy, AD = 43.2 Gy and a /b = 2 Gy is 47.5 Gy.

 It is thus suggested that in the case of a cobalt-60 thoracic irradiation with two parallel opposed AP fields at a dose of 36 Gy (following ICRU 29 specifications), the spinal cord is probably not at large risk for radiation myelitis, provided the two fields are treated together on each day. Let us now consider the (not 50 uncommon) situation where the fields are alternatively treated, the first day the anterior, the second the posterior, etc. The AD to the spinal cord is obviously unchanged: 9.9 Gy and 33.3 Gy are delivered by the anterior and the posterior field, respectively. However, full repair takes place between each fraction (separated by 24 h), and hence the BED must be calculated separately for the two fields: for D = 9.9 Gy, d = 1.1 Gy and a /b = 2 Gy, the BED is 7.67 Gy, the spinal cord receiving thus an effective dose smaller than the AD with the anterior field. For the posterior field, D = 33.3 Gy and d = 3.3 Gy which gives an equivalent dose of 47.4 Gy. The total BED  delivered  to  the  spinal  cord  is  thus 7.67 + 47.4 = 55.07 Gy which is certainly unacceptable and can result in a high incidence of radiation myelitis.

  The situation will be even worse with a cobalt-60 unit working at shorter SSD since the depth dose distribution is even poorer. Let us consider an old telecobalt unit with 50 cm SSD (not shown). In our present example, the spinal cord would lie on the 122% isodose, with a total AD of 44.1 Gy. Nine Gy would be given by the anterior field (50% isodose), and 35.1 Gy by the posterior field (195%). The BED would be 49 Gy if both fields were to be treated on each day (hot sched­ule!), and reach 58.45 Gy for alternative fields (totally indefensible if such a case were brought before the courts...)

 18 MV photon.  Following the same reasoning, a BED of 38.7 Gy vs. an AD of 37.8 Gy is delivered to the spinal cord when the two fields are simultaneously treated with 18 MV X-rays (Table III). In this case, it would be possible (if necessary) to increase the mid­plane dose up to 42-44 Gy without exceeding the safety limit, provided the two fields are simultaneously irradi­ated. For alternative fields, the BED rises to 42.5 Gy, which still remains within tolerance dose limits.

 Example 3

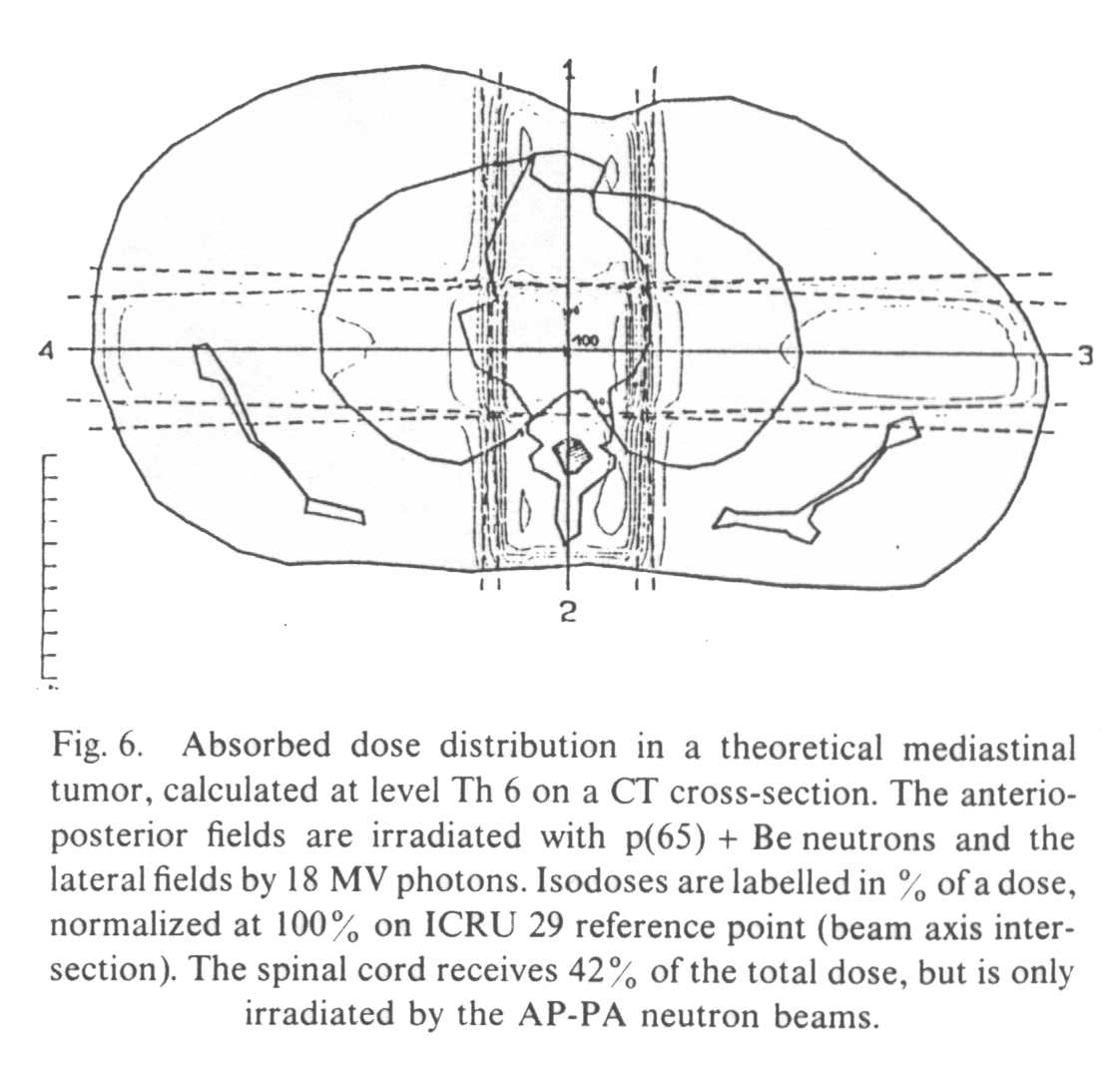
Figure 4 shows the absorbed dose distribution in an other CT plane (level Th 6), using a four field technique associating two AP parallel opposed neutron fields and two lateral parallel opposed 18 MV photon fields. This kind of beam arrangement is used in some neutron therapy centers in the treatment of gynecologic high stage pelvic tumors or prostatic adenocarcinoma and is occasionally proposed for bulky lung tumors (the case discussed here).

Neutron beams take their potential interest from their particular biological properties, and share these properties with all other high LET radiations. The important point here is that fractionation sensitivity is dramatically reduced with neutrons, as compared to gamma and X-rays. Indeed, data of the literature indi­cate almost uniformly high a /b values for normal tissues, i.e. higher than those quoted for low LET radiations. For instance, an a /b ratio of 23 Gy for lip mucosa [20] has been reported in biological murine systems. Studies in skin, kidney, colo-rectum and lung [14,17,21,22] have all demonstrated an approximately 10-fold increase in the a /b ratio for 3 MeV neutrons relative to X-rays. For fast neutrons of higher energy, such as those used in neutron therapy, a /b ratio are somewhat smaller, but still well above those determined from low-LET irradiations.

Therefore, since tissues characterized by a /b ratios of 10 Gy and more are little sensitive to fraction size alterations below 2.5-2 Gy, the BED calculated in our example with the LQ model are similar to the AD, at least for the AP neutron fields. In fact, the maximum increase in total dose, for a change in dose per fraction of 2 to i Gy, is only 3%, which falls in the range of uncertainty of neutron dosimetry. For the lateral photon fields, the situation is comparable to the one described in example 1.

Nevertheless, when planning a neutron treatment, practical reasons call for a kind of single average RBE value (sometimes called the clinical RBE, or the clinical neutron potency factor, CNPF) allowing for the calculation of "photon equivalent dose". This is a less than satisfactory solution, but such a simplification seems unavoidable in the clinical practice since, after all, a dose has to be prescribed. The limits of the con­cept of a photon equivalent dose must, however, be kept in mind, in order to avoid overdosage of sensitive nor­mal structures.

If no correction is needed for alterations in dose per fraction, it is essential to take into account the variation in RBE. Indeed, different RBEs have been reported for normal tissues when comparing fast neutrons to low LET radiations. These RBE values vary by a factor of 4, suggesting that the severity of different types of morbidity is likely to be different after neutron than after conventional radiotherapy (reviewed in ref. [3]). It is also a general (though not universal) finding that neutron RBEs for late effects are greater than for acute toxicity. This is connected with the use of fractionated irradiations in photon radiotherapy, which reduces the severity of late reactions.

In the present example, the neutron (n + y) dose has been converted in a photon equivalent dose using a clinical RBE of 2.8 Gy, determined from mouse jejunal crypt ceIl experiments. The rationale for this choice has been discussed elsewhere [11], but an important point is that this RBE refers to acute reactions. As usual, the isodoses are labeled in % of a total photon (lateral fields) and photon equivalent dose (AP fields). In the present case, the dose-limiting normal tissue is again the spinal cord. It can be seen from Fig. 6 that the spinal cord receives 75% of the total dose, i.e. 37.5 photon­equivalent Gy for a dose of 50 Gy prescribed at the intersection of the beam axes. On the other hand, the contribution of the photon lateral fields is only 2%, the spinal cord being irradiated only by the AP neutron fields.

If the clinical RBE of 2.8 has proven to be acceptable in the practice for most normal tissues (soft tissues, with an experience of now over 1200 patients in Louvain­-la-Neuve, UCL University), the RBE of the spinal cord, and more generally of the whole CNS, is much higher, and possibly as high as 5 [12]. It is thus essential to convert the photon equivalent dose calculated with RBE = 2.8 in a photon equivalent dose calculated with RBE = 5, i.e.:

 37.5 x 5 / 2.8 = 67 Gy

 Thus, the equivalent photon dose to the spinal cord is 67 Gy, obviously much higher than the 37.5 Gy calcu­lated with RBE = 2.8, and biologically totally unaccept­able.

An additional parameter also needs to be con­sidered, which is the gamma component of the neutron beam. It is, however, of unequal importance among the different neutron therapy facilities, as it depends on a number of factors (type and energy of particle acceler­ated, type 0f target, collimator, etc). We will not discuss it here, since it can be easily solved from the examples above. It is sufficient to know what is the gamma proportion of the (n + y) dose and to carry out the calculations separately for each component*.

 * In modem neutron therapy centers. this y component is smaller than 5% and can therefore be simply neglected

 Conclusion

 The conclusion is straight forward: isoeffect (or BED) calculations from computed ADD give a better insight into the biological impact of a radiotherapy treatment, and may improve the optimization procedures in treat­ment planning. Both the LQ model and the available clinical data on normal tissues repair capacity allow to do this in a wide range of situations, either with the actual a /b values derived for specific tissues or with average values of2 and 10 Gy for late and early reacting tissues, respectively. However, the following comment s need to be added:

 (1) Most of the tolerance levels of normal tissues have been defined in the past without a clearly stated dose per fraction, or assuming the same dose per fraction as the one prescribed at the 100% level (usually 2 Gy). Whether the normal tissues were actually irradiated at this 100% level remains, however, very frequently unclear. Moreover, tolerance levels are defined as ranges of doses rather than as clear dose thresholds, under which complications are not to be feared [19]. Absolute thresholds cannot be defined because of sev­eral factors, including individual variations between patients (age, sex, intercurrent diseases...), and the dif­ficulty to calculate retrospectively from series of patients what should be the total dose that a tissue can support without apparent damage. This remains thus a wide field of research for the future.

(2) No time factor was involved in this short overview, since we compared only different levels of dose per fraction within a single treatment, i.e. delivered by definition in the same total time. If the Wither's formula is to be used for comparison between different treatments, distributed among different total treatment times, a time factor must be included when relevant (early reacting tissues, or slow repair in late reacting tissue). Time factors have recently been discussed by Fowler, and the interested reader can best refer to his last paper on this subject [10].

(3) All these calculations have been done assuming a daily fractionation schedule, i.e. with intervals of 24 h between consecutive fractions. The formula is not valid for concentrated schedules where rep air may be incom­plete between consecutive fractions (where unrepaired sub lethal damage from a given fraction can interact with the following fraction), in which case the Incomplete Repair model of H. Thames [23] is probably the most appropriate approach which has been proposed, 50 far. (4) It is tempting to modify the presently available com­puter planning systems, by adding a routine calculating automatically the biological equivalents, as recently proposed by Beck Bornholdt et al. [2]. In our opinion, this should be envisaged with caution, since any misuse can lead to clinical disasters if, for example, wrong biological parameters are entered in the system. On the other hand, manual calculation, as presented here, makes one think about the biological meaning of any given dose and can be carried out on a small pocket­calculator. It is our opinion that a routine use of these corrections by the radiotherapist implies a good under­standing of the biological concept involved, as an important part of the general knowledge required for the practice of radiation oncology.

 References

 1      Barendsen, G. W. Dose fractionation, dose and isoeffect rela­tionships for normal tissue responses. Int. J. Radiat. Oncol. Biol. Phys. 8:1981-1997, 1982.

2      Beck-Bornholdt, H. P., Schmidt, R., Schwarz, R. C. and Hubener, K. H. Biological isoeffect distribution: consideration of the influence of dose per fraction and overall treatment time. A possible tool in future treatment planning. Radiother. Oncol., in press, 1991.

3      Bewley, D. K. The physics and radiobiology of fast neutron beams. Adam Hilger eds. Bristol & New York, 1989.

4      Chadwick, K. H. and Leenhouts, H. P. A molecular theory of cell survival. Phys. Med. Biol. 18: 78-87, 1973.

5      Cosset, J. M., Henry-Amar, M., Girinski, T., Malaise, E., Dupouy, N. and Dutreix, J. Late toxicity of radiotherapy in Hodgkin's disease. The role of fraction size. Acta Oncol. 27: 123-146, 1988.

6      Coutard, H. Roentgentherapy of epitheliomas of the tonsillar region, hypopharynx and larynx from 1920 to 1926. Am. J. Roentgol. 28:313-331, 1932.

7      Dutreix, J., Wambersie, A. and Bouhnik, C. Cellular recovery in human skin reactions: application to dose fraction number overall time relationship in radiotherapy. Eur. J. Cancer 9: 159-167,    1973.

8      Ellis, F. Fractionation in radiotherapy. In: Modem Trends in Radiotherapy, Vol. 1. Editors: T. J. Deeley and C. A. P. Wood. Buterworth, London, 1967.

9      Fowler, J. F. The linear-quadratic formula and progress in fractionated radiotherapy. Br. J. Radiol. 62: 679-694, 1989.

10   Fowjer, i F. How worthwile are short schedules in radio­therapy?: a series ofexploratory calculations. Radiother. Oncol. 18:165-182, 1990.

11   Gueulette, J. Thesis. Universite Paul Sabatier de Toulouse, 1978.

12   Hornsey, S. RBE for lung and cord. Int. J. Radiat. Oncol. Biol. Phys. 8: 2099-2102, 1982.

13   ICRU Report 29. Dose specification for reporting external beam therapy with photons and electrons. Washington, 1978.

14   Joiner, M. C., Maughan, R. L., Fowler, J. F. and Denekamp, J.      The RBE for mouse skin irradiated with 3 MeV neutrons: single and fractionated doses. Radiat. Res. 95:130-141, 1983. 15 Kellerer, A. M. and Rossi, H. H. The theory of dual radiation action. Curr. Top. Radiat. Res. Q. 8: 85-158, 1972.

16   Lauk, S., Ruth, S. and Trott, K.-R. The effect of fractionation on radiation-induced heart disease in rats. Radiother. Oncol. 8: 363-368, 1987.

17  Parkins, C. S., Fowler, J. F., Maughan, R. L. and Roper, M. J. Repair in mouse lung for up to 20 fractions of X-rays or neutrons. Br. J. Radiol. 58: 225-241, 1985.

18   Regaud, C. and Ferroux, R. Discordance des effets des rayons X, d'une part dans le testicule, par le fractionnement de la dose. C. R. Soc. Biol. 97: 431, 1927.

19   Rubin, P. Law and Order of radiation sensitivity. In: Front. Radiat. Ther. Oncol., Vol. 23, pp. 7-40. Editors: J. M. Vaeth and J. L. Meyer. Karger, Basel, 1989.

20   Scalliet, P. Investigation of repalr characteristics in early and late responding tissues. Comparison of fractionated and low dose rate experiments. Thesis, University of Leuven, in press, 1991.

21   Stewart, F. A., Soranson, J. A., Maughan, R., Alpen, E. L., Williams, M. V. and Denekamp, J. The RBE for renal damage alter irradiation with 3 MeV neutrons. Br. J. Radiol. 57: 1009-1021, 1984.

22   Terry, N. H. A. and Denekamp, J. RBE values and repair char­acteristics for colo-rectal injury alter cesiurn- 137 gamma-ray and neutron irradiation. Il.   fractionation up to 10 doses. Br. J. Radiol. 57: 617-629, 1984.

23 Thames, H. D. An incomplete repair model for survival after fractionated and continuous irradiation. Int. J. Radiat. Biol. 47: 319-339,       1985.

24   Thames, H. D. and Hendry, J. H. Fractionation in Radio­therapy. Taylor & Francîs London - New York - Philadelphia, 1987.

25 Thames, H. D., Bentzen, S. M., Turesson, I., Overgaard, M. and van den Bogaert, W. Time-dose factors in radiotherapy: a review of the human data. Radiother. Oncol. 19: 219-236, 1990.

26 Van der Schueren, E., Landuyt, W., Ang, K. K. and Van der Kogel, A. J. From 2 to 1 Gy per fraction: sparing effect in rat spinal cord. Int. J. Radiat. Oncol. Biol. Phys. 14: 297-300, 1988.

27   Van Rongen, E., Madhuizen, H. T., Tan, C. H. T., Durham, S. K. and Gijbels, M. J. J. Early and late effects of fractionated irradiation and the kinetics of repair in rat lung. Radiother. Oncol. 17: 323-337, 1990.

28   Vynckier, S., Pihet, P., Flemal, J. M., Meulders, J. P. and Wambersie, A. Improvement of a p(65) + Be neutron beam for therapy at Cyclone, Louvain-la-Neuve. Phys. Mcd. Biol. 28: 685-691, 1983.

29 Withers, H. R., Thames, H. D. and Peters, L. J. A new isoeffect curve for change in dose per fraction. Radiother. Oncol. I: 187-191,  1983.

 Appendix

Withers [29] calculated the isoeffect formula as follows:

We already known that the relationship between any biological effect E and the radiation dose D can be described by the LQ model:

E = aD + bD²

If the dose D is delivered in n fractions of size d, the formula becomes

E = a (nd) + b (nd)², with D = nd.

If we try to find out a new schedule, with a new dose per fraction d', equivalent to a known reference sched­ule (i.e. isoeffective with this reference treatment) delivered in n fractions of size d, we may write:

E         = a (nd') + b (nd' )² is equivalent to E = a (nd) + b (nd)²,

therefore, since the effect E is intended to be the same,

a (nd) + b (nd)² = a (nd') + b (nd' )²

This formula can be very simply converted, into the one published by Withers: